https://ac.nowcoder.com/acm/contest/881/F

题意：给一个三个顶点确定的三角形 内有一随机点p 求期望E=MAX{Spab,Spac,Spbc}

先回顾一下三角形的几个心：

重心：
1.中线的交点
2.到顶点和对边的距离为2：1
3.为三点坐标的算术平均值
4.组成的三角形相等

外心：
1.垂直平分线的交点
2.到三点距离相等

垂心：
1.高的交点
2. 三角形外心O、重心G和垂心H三点共线，且OG︰GH=1︰2。（此直线称为三角形的欧拉线（Euler line））（除正三角形）

内心：
1.∠平分线交点
2.到三边的距离相等

再看看这个题。。。好像没啥好说的。。。感觉这种数学题真的很看感觉。。。一般要拿一个正三角形去证明一下 过程如下 就是把群里大佬的做法又抄了一遍
充分利用对称性啊喂（茫然

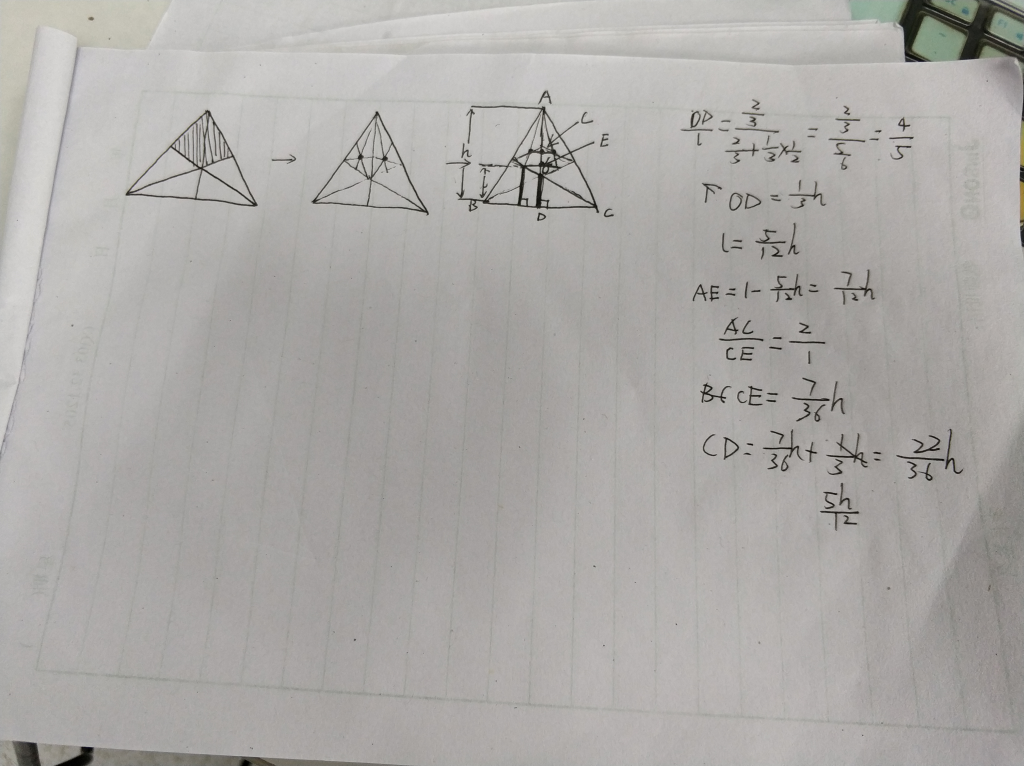
#include<algorithm>
#include<iostream>
#include<vector>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<ctime>
#include<map>
#include<stack>
#include<set>
#include<cstring>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;
const int INF = 0x3f3f3f3f;
 
ll cal(ll x1, ll y1, ll x2, ll y2, ll x3, ll y3) {
    return abs((x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1))*11;//叉乘结果*0.5（面积）*36（题目要求）*22/36（推出来的）=11
}
 
int main()
{
    ios::sync_with_stdio(0);
    ll x1, y1, x2, y2, x3, y3;
    while (cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3) {
        cout << cal(x1, y1, x2, y2, x3, y3) << endl;
    }
    return 0;
}