http://poj.org/problem?id=2559

题目大意：一堆宽为1 高可变的矩形凑在一起 求最大矩形是多大

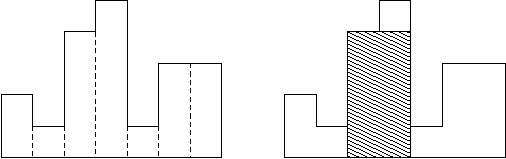
思路 单调栈 用两次 从左到右 和从右到左 求出每个矩形的左右最长延伸度
最后再过一遍 求出最大面积即可 2 1 5 6 1 3 3为例 我们画一下栈 帮助理解这个题。编号分别是1 2 3 4 5 6 7
一开始
2 入栈 第一块左为0 栈为1
1入栈 第二块左为0 栈为2
5 入栈 第三块左为2 栈为2 3
6 入栈 第四块左为3 栈为2 3 4
1 入栈 第五块左为0 栈为5
3 入栈 第六块左为5 栈为5 6
3 入栈 第七块左为5 栈为5 7

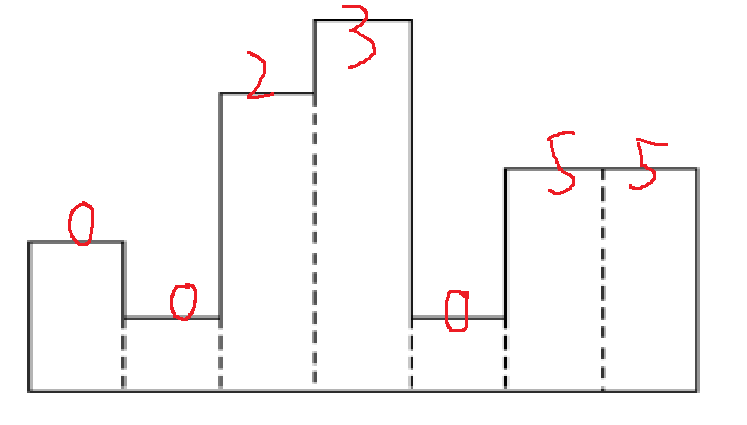
之后我们在倒着从后往前找右边的边界
3 入栈 第七块 右为8 栈为7
3 入栈 第六块 右为8 栈为6
1 入栈 第五块 右为8 栈为5
6 入栈 第四块 右为5 栈为5 4
5 入栈 第三块 右为5 栈为5 3
1 入栈 第二块 右为8 栈为2
2 入栈 第一块 右为2 栈为1

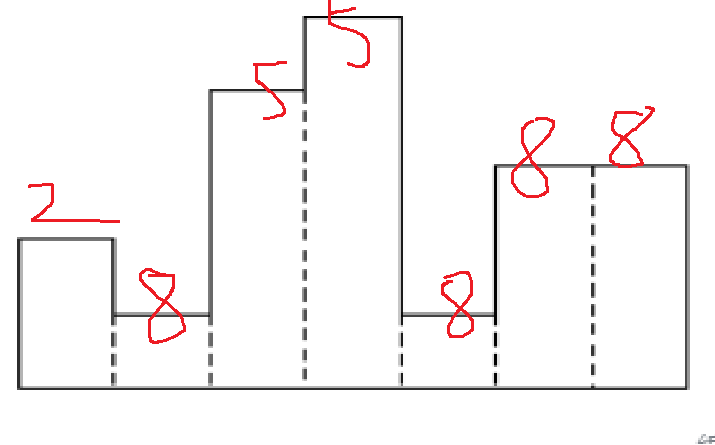
根据以上两图可以计算出每个矩形的最大面积为
2 7 8 5 7 6 6

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <stack>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
int arr[maxn], l[maxn], r[maxn];

int main()
{
    int n;
    ll ans = 0;
    stack<int> st;
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &arr[i]);
    }
    for(int i = 0; i < n; i++) //寻找每个矩形的左边界 保证严格递增
    {
        while (!st.empty() && arr[st.top()] >= arr[i]) //非空且新的值小于等于当前栈顶的值
        {
            st.pop();
        }
        if (st.empty())
            l[i] = 0;
        else
            l[i] = st.top()+1;
        st.push(i);
    }
    while (!st.empty())
    {
        st.pop();
    }
    for (int i = n - 1; i >= 0; i--)//找右边
    {
        while (!st.empty() && arr[st.top()] >= arr[i])
            st.pop();
        if (st.empty())
            r[i] = n;
        else
            r[i] = st.top();
        st.push(i);
    }
    for (int i = 0; i < n;i++){
        //cout << r[i] << ' ' << l[i] << endl;
        //cout << (ll)arr[i] * (r[i] - l[i]) << endl;
        ans = max(ans, (ll)arr[i] * (r[i] - l[i]));
    }
    cout << ans << endl;
    return 0;
}