原题链接:https://www.acwing.com/problem/content/1249/
给定了n个加号 m个减号 n+m+1个数字 问怎样用这些数字和运算符组合 组合出来的结果最大
首先看一下后缀表达式百度给出的定义
- 如果E是一个变量或者常量,那么E的后缀式就是E本身
- 如果E是E1 op E2形式的表达式,这里op是任何二元操作符,则E的后缀式为E1'E2'op,这里E1'和E2'分别是E1和E2的后缀式
- 如果E是(E1)形式的表达式 那么E1的后缀式就是E的后缀式
当年的想法
当年看到这个题的时候 完全没有考虑后缀表达式这个东西 想的就是最菜的贪心 正数尽量大的相加 负数绝对值越大的相减 最后整出一个答案来 也没管对错啥的 赛后xky给我讲 这个题不是这样做的 是和后缀表达式有关的 我也没多想... 那么现在认真的分析一下这道题
正解
首先 后缀表达式可以表示成一棵树 比如 45+32-- 这个式子 可以表示成
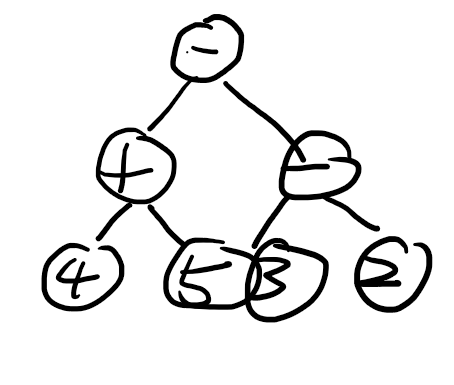
这颗树对应的后序遍历就是后缀表达式 树的前中后序表达式就是前中后缀表达式
然后我们得考虑 给了n个加号和m个减号 是不是就固定了
我们拿a b c d e五个数字和四个减号做例子
最朴素的组合是这样的

之后我们进行变换(对树的结构)

我们可以看到 这样减号的数量一下子从4个变成了一个 我们再加一颗树(我就是想画画)
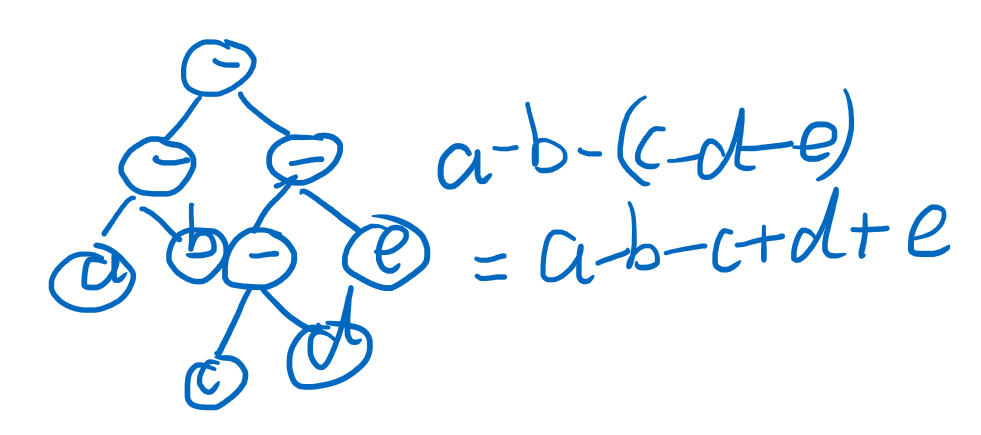
因此我们可以得知 后缀表达式中更改树的结构 实质上就等于给中缀表达式加括号
同理可得 在存在减号的情况下 加号也可以变成减号 也就是
给定n+m个加减号 实质是减号的个数可以在1-n+m之间随意的变换
在得出该定理之后 我们再看这个题
不难想明白
如果没有负号 那么将所有的数字加起来就行了(因为加号没有办法改成符号)
如果有符号 第一个数字一定是正的 所以说 第一个数是最大的数字 然后减去最小的数字 对于其他的数字 正加负减就行了(我当时想能不能只去找最小值 实际上如果全是负数的话 就会出错了)
代码
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
#define x first
#define y second
typedef long long ll;
typedef pair<int, int> PII;
const int maxn = 110;
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 10;
int arr[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 0; i < n + m + 1; i++)
{
cin >> arr[i];
}
ll ans = 0;
sort(arr, arr + n + m + 1);
if (m == 0)
{
for (int i = 0; i < m + n + 1; i++)
{
ans += arr[i];
}
}
else
{
ans = arr[n + m] - arr[0];
for (int i = 1; i < m + n; i++)
{
ans += abs(arr[i]);
}
}
cout << ans << endl;
return 0;
}










Comments | NOTHING