1.归并排序
int q[maxn], w[maxn];//q为原数组 w为临时数组
void merge_sort(int l, int r) {//归并的左右界限
if (l >= r) return;//如果只剩一个元素 返回
int mid = l + r >> 1;//否则寻找中点
merge_sort(l, mid);//递归左半部分
merge_sort(mid + 1, r);//递归右半部分
//归并过程
int i = l, j = mid + 1, k = 0;//左右两个数组 i指向左边的数组的第一个 j指向右边数组的第一个 k为了方便从0开始
while (i <= mid && j <= r) {//当i j均未结束的时候
if (q[i] < q[j]) w[k++] = q[i++];//将小的归到w数组中
else w[k++] = q[j++];
}
while (i <= mid) w[k++] = q[i++];//如果i未结束 继续加入 可以简单证明一定是最大的
while (j <= r)w[k++] = q[j++];//同理
for (i = l, j = 0; i <= r; i++, j++) {//i是这一段数组(无序) j指向我们刚刚操作完毕的w数组 将w数组放入到q数组当中 保证q数组的这一部分变得有序 第二个条件可以改成j<k 一个道理
q[i] = w[j];
}
}
2.前缀和和差分
“下次你路过,人间已无我,但我的国家,依然是五岳向上,一切江河依然是滚滚向东,民族的意志依然向前,向着热腾腾的太阳,跟你一样。” ----余光中
十分基础的知识了 一直没有整理一下
前缀和和差分可以说是互逆的算法
前缀和用来解决一个数组多次查询某区间值
差分用来解决多次修改后查数组
一个偏向于差一个偏向于改 两者兼顾要用树状数组
应用这两种算法时 一般数组从1开始用
一位前缀和和二维前缀和
原数组为a[i]
建立数组b[i],使得b[i]=a[1]+a[2]+...+a[i]
求和的时候用b[r]-b[l-1]快速求和
for (int i = 1; i <= n;i++){
cin >> a[i];
}
for (int i = 1; i <= n;i++){
b[i] = b[i - 1] + a[i];
}
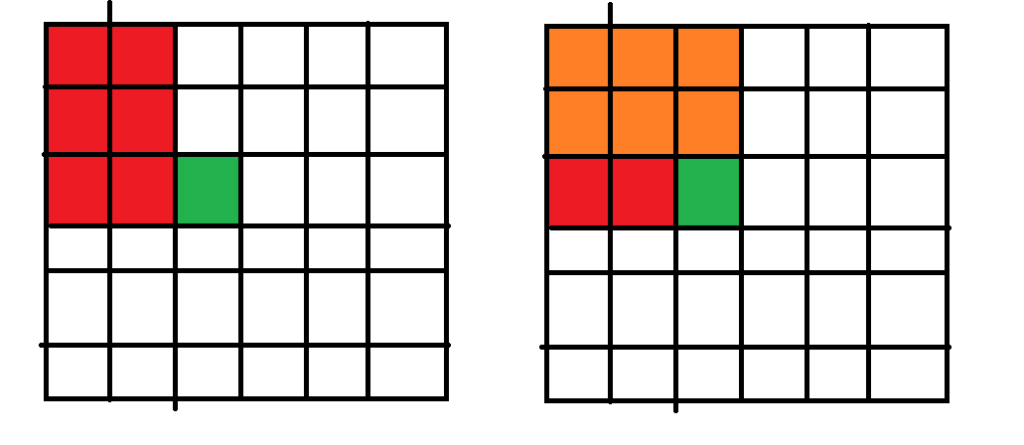
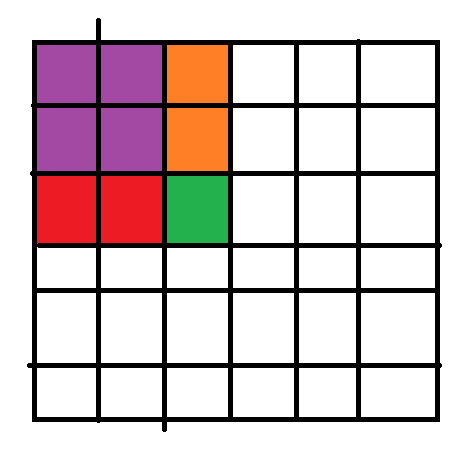
关于二维前缀和要使用容斥原理 如图所示 要求绿色格子的值 先要把红色部分的值加上 再加上橙色部分的值 此时发现加多了一块 图三标识为紫色 再减去紫色 同时加上绿色格子本身的值即可 查询的时候同理 看代码
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
b[i][j] = b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1] + a[i][j];
}
}
while (q--) //查询
{
int x1, y1, x2, y2; //这里假定x1 y1为左上角 x2 y2为右下角的值
cin >> x1 >> y1 >> x2 >> y2;
int ans = b[x2][y2] - b[x1 - 1][y2] - b[x2][y1 - 1] + b[x1 - 1][y1 - 1];
cout << ans << endl;
}
差分
原数组是a[]
构造一个数组b[] 使得a[i]=b[1]+b[2]+...+b[i] 具体如何构造我们不关心 假设一开始a中所有元素都是0 只需要将a每个位置加上a[i]即可
建议修改写成一个函数
如果修改a[l]-a[r] 每个加上1 修改b[r+1]-=c b[l]+=c即可
void insert(int l,int r,int c){
b[l] += c;
b[r + 1] -= c;
}
int main(){
cin >> n >> m;
for (int i = 1; i <= n;i++){
cin >> a[i];
insert(i, i, a[i]);//插入原数组
}
for (int i = 0; i < m;i++){//修改
int l, r, c;
cin >> l >> r >> c;
insert(l, r, c);
}
for (int i = 1; i <= n;i++){
a[i] = a[i - 1] + b[i];
cout << a[i] << ' ';
}
return 0;
}
二维差分
注意二维差分的插入操作的写法 一个格子加了c 对应的效果是他的右下方全部加了c
void insert(int x1,int y1,int x2,int y2,int c){
b[x1][y1] += c;//左下方全部加上
b[x1][y2 + 1] -= c;//下面减去
b[x2+1][y1] -= c;//左边减去
b[x2 + 1][y2 + 1] += c;//加回重复减去的
}
int main(){
ios::sync_with_stdio(0);
cin >> n >> m >> q;
for (int i = 1; i <= n;i++){
for (int j = 1; j <= m;j++){
cin >> a[i][j];
insert(i, j, i, j, a[i][j]);
}
}
int x1, x2, y1, y2, c;
for (int i = 0; i < q;i++){
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
for (int i = 1; i <= n;i++){
for (int j = 1; j <= m;j++){
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];//求前缀和和前面一样
cout << a[i][j] << ' ';
}
cout << endl;
}
}
3.二分查找
int bs(int l, int r)
{ //分成[l,mid] [mid+1,r] r=mid/l=mid+1
while (l < r)
{
int mid = l + r >> 1;
if (check(mid))
r = mid;
else
l = mid + 1;
}
return l;
}
int bs(int l, int r)
{ //分成[l,mid-1] [mid,r] r=mid+1/l=mid
while (l < r)
{
int mid = l + r + 1 >> 1; //注意这里的加1
if (check(mid))
l = mid;
else
r = mid - 1;
}
return l;
}
4.素数筛
在O(n)的时间复杂度中求出1-n中的所有素数
素数(质数):因子(在大于1的自然数中)只有1和本身的数
普通筛法中,一个和数可能被多个素数筛掉 比如6 被2筛一次 又被3筛一次 浪费了时间复杂度 线性筛法中将合数表示成最小素数*一个数的形式
枚举到i 设p是i的最小质因子 p1<p2<...<p(全是质数) 将p1*i,p2*i,...p*i标记为合数 这样能保证一个数字只被筛掉一次
int primes[N], cnt; //primes存素数 cnt计数
bool st[N]; //st记录该数是否是素数
void get_primes(int n)
{
for (int i = 2; i <= n; i++) //从2开始
{
if (!st[i])
primes[cnt++] = i; //如果该数是素数 那么将其加入primes数组
for (int j = 0; primes[j] * i <= n; j++)//之后筛掉倍数
{
st[primes[j] * i] = true;//标记
if (i % primes[j] == 0)//已经筛到p了
break;
}
}
}










Comments | NOTHING